redis管道 发布订阅 事务
本文共 1495 字,大约阅读时间需要 4 分钟。
可以通过如下网址学习redis
http://redis.cn/ 命令–>bitcount 文档–>redis使用、redis管理 主从复制 高可用 集群1.nc命令
yum install nc 建立socket连接:nc命令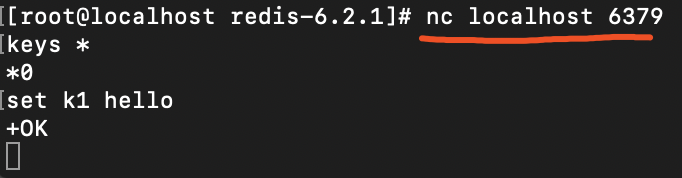 连接到客户端,可以看到上面创建的k1。因此若没有redis客户端,通过nc命令也是可以执行的。
连接到客户端,可以看到上面创建的k1。因此若没有redis客户端,通过nc命令也是可以执行的。  2.管道 管道:将多个命令 放到一个管道,降低通信成本
2.管道 管道:将多个命令 放到一个管道,降低通信成本 [root@localhost redis-6.2.1]# echo -e “abc\ncdf”
abc cdf [root@localhost redis-6.2.1]# echo -e “set k2 99\n incr k2\n get k2” | nc localhost 6379 +OK :100 $3 100
3.冷启动
文档–>从文件中批量插入数据 redis冷启动: server> cat d1.txt | redis-cli4.发布订阅
redis发布订阅:订阅以后,发送的消息才会实时收到。 只要订阅了此消息,发送者发送的消息 都会看到。客户端1推送消息:
127.0.0.1:6379> PUBLISH k1 hello
(integer) 0
客户端2订阅消息
127.0.0.1:6379> SUBSCRIBE k1
Reading messages… (press Ctrl-C to quit)
- “subscribe”
- “k1”
- (integer) 1
- “message”
- “k1”
客户端1再发生消息:
127.0.0.1:6379> PUBLISH k1 helloworld
(integer) 1
客户端2 实时收到此消息:
127.0.0.1:6379> SUBSCRIBE k1
Reading messages… (press Ctrl-C to quit)
- “subscribe”
- “k1”
- (integer) 1
- “message”
- “k1”
- “helloworld”
微信群可以查看历史聊天机构:
历史聊天记录存在什么地方? 数据全量在数据库,一般用redis做缓存。获取数据:实时性数据采用发布订阅模式存储,历史性数据采用sorted set存储,更老的数据放入数据库。
写入数据: 方案1:客户端分别调 发布订阅、sorted_set、发送给kafka 慢慢写入数据库。问题:发送给发布订阅后,客户端挂掉。 方案2:三台redis,一台负责发布订阅,第二台也订阅此主题,收到消息后发送给sorted_set;第三台也订阅此主题,收到消息后,发送给kafka,由kafka写入数据库。 zremrangebyrank 时间作为分值 消息作为元素 help @sorted_set 查看此结构的用法
zremrangebyrank 时间作为分值 消息作为元素 help @sorted_set 查看此结构的用法 两个redis保证消息落库不丢失。
 另一个是用事务。
另一个是用事务。 5.redis事务
 multi 是开启事务的命令;exec是发送的命令结束的指令 此命令发送后 开始执行命令。
multi 是开启事务的命令;exec是发送的命令结束的指令 此命令发送后 开始执行命令。 127.0.0.1:6379> MULTI
OK 127.0.0.1:6379(TX)> set k1 aaa QUEUED 127.0.0.1:6379(TX)> set k2 bbb QUEUED 127.0.0.1:6379(TX)> EXEC
- OK
- OK
谁的exec先到达,会先执行谁的命令:
 watch: 会在multi命令前,先发送watch命令,意思是监控。 如监控此时k1为2,黄色客户端命令改变k1的值时,后续绿色的再获取k1的值,会不执行,绿色的事务会消失。
watch: 会在multi命令前,先发送watch命令,意思是监控。 如监控此时k1为2,黄色客户端命令改变k1的值时,后续绿色的再获取k1的值,会不执行,绿色的事务会消失。 

转载地址:http://iwvhz.baihongyu.com/
你可能感兴趣的文章